Les ordinateurs quantiques

Depuis plusieurs années, on entend beaucoup parler des ordinateurs quantiques et des fabuleuses possibilités qu’ils seraient en mesure de nous offrir. Entre boites magiques capables de répondre à toutes nos questions et ordinateurs surpuissants reléguant nos machines actuelles au rang de dinosaures, il nous semblait judicieux de revenir sur quelques points concernant cette technologie qui pourrait devenir une des innovations majeures de cette année 2017.
Fonctionnement des ordinateurs quantiques :
Afin de mesurer les effets et avancées que représenteraient la maîtrise des ordinateurs quantiques, il est important de survoler rapidement leur fonctionnement de base.
En informatique classique, la puissance de calcul de nos machines est définie grâce au “bit”, la plus petite quantité d’information possible, pouvant prendre la valeur 0 ou 1. Nos ordinateurs sont des ensembles de transistors, traversés par un courant électrique, chaque transistor pouvant prendre ces fameuses valeurs 0 ou 1. Ainsi, l’ensemble des programmes sur nos machines, depuis le traitement de texte jusqu’à l’exécution de jeux s’effectuent en interne grâce à ces bits, sur lesquels on agit grâce à différentes opérations. Pour augmenter la puissance de calcul, il faut alors simplement augmenter le nombre de bits (afin de traiter plus d’information) tout en qu’augmentant également la mémoire (permettant de stocker ces informations). Cependant, cette puissance de calcul de nos ordinateurs (qui peut nous paraître déjà élevée) est absolument dérisoire face à celle de l’informatique quantique…
Alors que nos ordinateurs classiques calculent à partir de bits pouvant prendre les fameuses valeurs 0 et 1, les ordinateurs quantiques se servent de « qubits », obéissant aux règles de la physique quantique. Il n’est ainsi plus question de courant électrique simulant les 2 valeurs du code binaire, mais d’électrons, photons, ions ou noyaux atomiques, qui suivent les principes fondamentaux de l’intrication et de la superposition quantique.
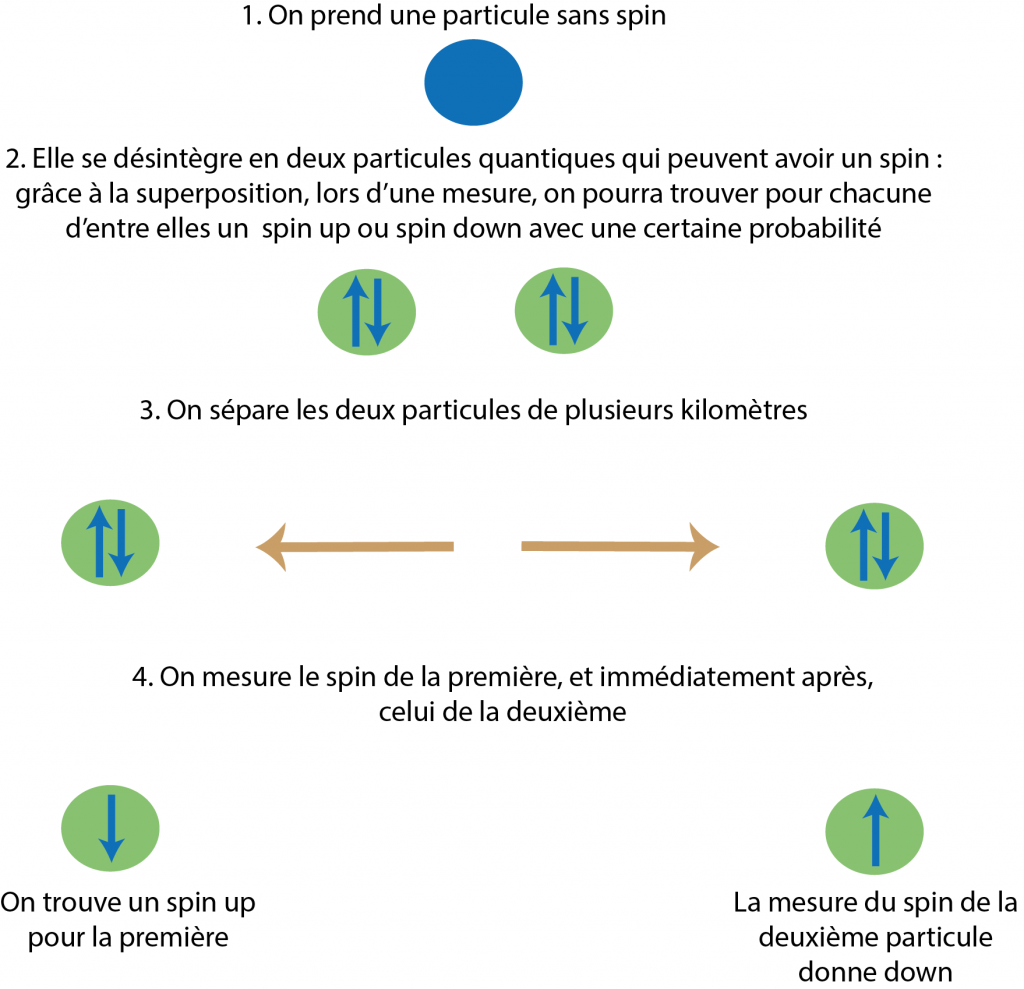
Juste avant de voir ces phénomènes, il est important de définir le spin d’une particule. Très schématiquement et très simplement, le spin d’une particule est l’une de ses caractéristiques (comme la masse ou la charge électrique) pouvant être représentée à notre échelle macro comme sa rotation. Alors même si la particule ne “tourne” pas vraiment au sens physique du terme, c’est la dénomination qui s’en rapproche le plus pour caractériser ses effets. En effet, une fois placée dans un champ magnétique, la particule va être déviée comme un aimant, ce qui nous permet de lui donner une valeur : positive ou négative.
L’intrication est donc un phénomène définissant le spin de 2 particules, même très éloignées l’une de l’autre, de sorte que si l’on mesure le spin de l’une, on peut connaitre le spin de l’autre (qui sera négatif si le premier est positif et inversement). Cette propriété contre-intuitive due à une transmission d’informations qui dépasserait la vitesse de la lumière permet pourtant de définir ces particules intriquées comme faisant partie d’un même système. On peut alors lier plusieurs systèmes éloignés, pouvant apparaître de prime abord comme étant indépendants. Cette propriété est ainsi très importante pour la transmission d’informations (le copier/coller n’existant pas sur les ordinateurs quantiques comme nous le verrons plus tard).
Mais c’est surtout la deuxième propriété quantique dont on entend souvent parler dans le cas de l’ordinateur : la superposition quantique. En effet, quand on interroge un bit classique sur son état, il nous renvoie la valeur 0 ou 1. Cependant, on ne peut pas poser la même question à un qubit qui peut prendre une infinité de valeurs différentes de 0 et 1. C’est pour cette raison que l’on a tendance à simplifier en disant abusivement que le qubit est dans « deux états à la fois » et qu’il est à la fois 0 et 1. Cet énoncé n’a pourtant bien évidement aucun sens physique : le système est dans son état propre qui est toujours le même !
Cependant, comme on ne peut connaitre cet état, on lui demande s’il est dans des états que l’on peut connaitre (0 et 1). Ainsi, à la question es-tu dans l’état 0, ou es-tu dans l’état 1, le qubit répondra l’un ou l’autre, aléatoirement. Aléatoirement certes mais pas au hasard pour autant, puisque la distribution des résultats suivra une loi de probabilité, l’état de la particule étant « plus ou moins proche » de 0 ou de 1. On dit aussi que son état est une combinaison ou une superposition de 0 et de 1 (0 et 1 étant des états de référence arbitraire, la réalité physique ne définissant bien sûr aucun état « primaire » dont les autres ne seraient que des combinaisons).
L’ordinateur quantique calcule donc suivant ces distributions probabilistes ce qui permet, au lieu de 2 états d’en avoir une infinité. De plus, l’état d’un système regroupant plusieurs qubits n’est pas seulement une combinaison des états respectifs des qubits. Un assemblage de 2 qubits peut ainsi prendre 4 états différents « en même temps » (bien que vous ayez compris que c’est un abus de langage, un chat ne pouvant être vivant et mort ! #Schrödinger). Ainsi, la puissance de calcul double en fait à chaque fois que l’on ajoute un qubit, l’ordinateur disposant d’une puissance de calcul de 2^n pour n qubits !
C’est cette puissance gigantesque qui a tendance à exciter l’imagination lorsque l’on parle d’ordinateur quantique et que l’on pense à nos simples appareils à 64 bits (64 qubits représenteraient la capacité de calcul de 18 000 000 000 000 000 000 bits) …
Cependant, c’est là une lourde erreur que de croire ce dernier résultat exact, l’incroyable capacité de calcul du qubit étant limitée…
Limites des ordinateurs quantiques :
Eh oui, il n’y a malheureusement peu de chances que nos machines passent dans la prochaine décennie à des processeurs 64 qubits nous permettent de faire des tonnes d’opérations en parallèle. En effet, on ne peut jamais comparer les éléments quantiques à nos éléments à l’échelle macro et on ne peut ainsi faire le raccourci qubit = bit dopé !
Quand bien même nos machines personnelles pourraient accueillir la formidable complexité qu’exigent les ordinateurs quantiques, qui doivent être capables d’isoler les particules et composants du monde extérieur en étant refroidis à des températures proches du 0 absolu, il reste que la puissance de calcul ne fonctionne que pour les calculs intermédiaires…
En effet, à partir du moment où l’on demande au qubit de se positionner et de définir s’il est 0 ou 1, il perd totalement sa propriété de superposition qui lui conférait ces avantages pour ne devenir qu’un « simple bit » avec ses valeurs 0 ou 1. Ce phénomène d’effondrement quantique conduit l’ordinateur quantique à rester un instrument avec des domaines d’application assez limité puisque pour pouvoir exploiter pleinement la formidable puissance de calcul de la machine, il faut concevoir des algorithmes nécessitant d’importants calculs intermédiaires et non des séries de calculs en parallèle. C’est l’un des effets les plus frustrants de l’informatique quantique puisque l’on ne peut pas réfléchir de manière classique, et juste utiliser ces nouvelles machines comme des super-ordinateurs. On doit penser et réfléchir les algorithmes de manière quantique sous peine de se retrouver avec un simple ordinateur classique, ne pouvant pas faire mieux tourner nos programmes que les machines actuelles.
Le bouleversement de la cryptographie
Un de ces algorithmes quantiques les plus connus (étant également un des seuls) est l’algorithme de Shor, permettant de décomposer des nombres en facteurs premiers.
Pour comprendre l’incroyable bouleversement que pourrait provoquer cet algorithme s’il arrivait à tourner sur un ordinateur quantique, il faut savoir que le système de chiffrement le plus répandu actuellement et sécurisant la plupart de nos opérations en ligne est le système RSA. Ce système fonctionne au moyen de nombres premiers très grands. Ainsi, pour hacker ce système, il « suffit » de décomposer ces nombres en facteurs premiers. La force de ce système de cryptage est qu’il n’existe encore actuellement aucun super-ordinateur capable de le faire en temps réel. Cependant, l’algorithme de Shor remettrait en question l’inviolabilité de ce système et les premiers à maîtriser cet outil auraient en théorie la clé ultime de toutes les informations aujourd’hui cryptées ! C’est ainsi l’ensemble de nos données personnelles, mails, achats sécurisés et autres qui seraient menacées ! On comprend dès lors que l’on a retrouvé dans les documents leakés par Edward Snowden la mention des ordinateurs quantiques dans les recherches de la NSA afin d’infiltrer même les cibles les plus difficiles…
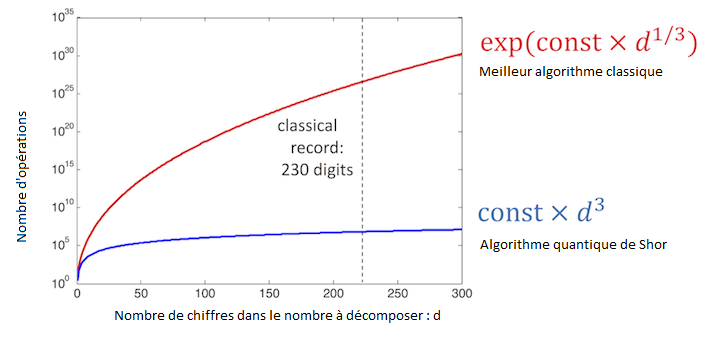
Crédit: Institut Pandore
Cependant, bien qu’effrayante, cette possibilité pourra ensuite être contrecarrée par la cryptographie quantique. En effet, grâce au caractère probabiliste du qubit, il est impossible de copier/coller une information. De plus, les propriétés quantiques font que si l’on tente d’observer un système de particules, on les altère en les fixant dans un état (le fameux principe d’effondrement quantique). Ces 2 caractères sont utilisés en cryptographie quantique pour assurer la confidentialité absolue des informations, un hacker modifiant l’information au moment où il la voit, et ne pouvant pas la copier.
Vous avez maintenant une idée générale de la façon dont fonctionnent ces calculateurs quantiques ainsi que leurs principaux avantage mais aussi limites et domaines d’application. Cependant, si vous désirez prolonger quelque peu la réflexion et vous demander si ces machines pourraient résoudre un des plus grands problèmes mathématiques de l’Histoire, je vous invite à lire attentivement la prochaine partie.
P=NP ?
Bien que la cryptographie soit l’un des domaines les plus populaires pour illustrer les applications de l’informatique quantique, ces appareils pourraient également nous permettre d’améliorer nos connaissances en physique quantique ainsi qu’en mathématiques.
Ainsi, certains avanceraient que les ordinateurs quantiques pourraient être la solution pour prouver que P=NP ou que P≠NP.
Pour bien comprendre la révolution que cela serait, il faut savoir que le problème P=NP est l’un des plus grands problèmes mathématiques et que prouver cette conjecture apporterait, certes 1 million de dollars de la part de l’Institut de mathématiques Clay, mais révolutionnerait également de nombreux domaines comme l’ingénierie, l’économie, la météorologie, la cryptologie, l’informatique et bien sûr, les mathématiques.
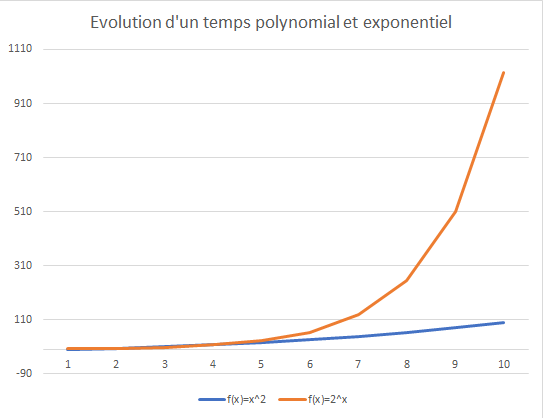
Les problèmes de classe P sont ceux qui peuvent se résoudre selon un temps Polynomial. C’est donc un temps « rapide », gérable à l’échelle humaine avec les capacités de nos ordinateurs actuels (le temps de résolution peut par exemple augmenter en suivant la fonction n^2, n étant le nombre de données d’entrée).
Cependant, il existe des problèmes comme le problème du voyageur de commerce (un problème d’optimisation où l’on cherche le plus court chemin pour passer une seule fois par toutes les villes d’une carte ainsi que la ville de départ), dont le temps de recherche d’une solution augmente de façon exponentielle (le temps de résolution peut par exemple augmenter en suivant la fonction 2^n, n étant le nombre de données d’entrée). Ces types de problèmes sont dit de classe NP (nondeterministic polynomial time) et ne peuvent se résoudre grâce à nos algorithmes sur nos ordinateurs actuels car le temps de traitement pour trouver la réponse est trop long. La deuxième particularité de ces problèmes est que la vérification d’une solution prend peu de temps (comprendre s’effectuer dans un temps polynomial). Ainsi, si chercher la réponse peut être ardu, la vérifier est beaucoup plus simple !
Enfin, il existe une catégorie spéciale de problèmes NP que sont les problèmes NP-complets. Ce sont les plus difficiles parmi les problèmes NP mais présentent l’avantage de tous poser la même question mathématique, sous des énoncés différents. Ainsi, si l’on trouve un algorithme “efficace” (soit dans un temps polynomial) pour résoudre un de ces problèmes NP complet, on sera en mesure de résoudre “efficacement” (donc dans un temps polynomial) l’ensemble des problèmes de classe NP.
Or, si l’on peut résoudre les problèmes de classe NP dans un temps polynomial, c’est que ce sont des problèmes de classe P (selon la définition même de la classe P). On aurait donc montré que NP=P.
Les ordinateurs quantiques pourraient nous aider à prouver cet énoncé et certains spécialistes pensent que la réponse viendrait d’un algorithme quantique, encore à découvrir.
Cependant, si P≠NP comme cela est désormais partagé par de nombreux spécialistes, certains espèrent que les ordinateurs quantiques nous permettront quand même de trouver une solution en temps polynomial aux problèmes NP.
En effet, puisqu’il est « facile » de vérifier la validité d’une solution proposée aux problèmes NP, et que l’on sait que la puissance de calcul d’un ordinateur quantique est, elle aussi, exponentielle, on peut supposer qu’il suffit de tester toutes les solutions possibles et de voir laquelle est la bonne…
Pour un nombre de solutions possibles S, on se rend compte que la moyenne de temps passé pour trouver une solution avec cette méthode est de S/2 multiplié par le temps (polynomial) de vérification d’une solution.
Rien d’impossible donc si l’on dispose d’une puissance de calcul suffisante….
Cependant, on doit là encore faire face au problème fondamental de l’ordinateur quantique qu’est l’effondrement quantique. Impossible de faire tous ces calculs en parallèle ! Ainsi, il faut réussir à trouver un algorithme quantique qui exploite la structure du problème pour pouvoir se servir de la puissance de calcul quantique, comme a pu le faire Shor (même si la factorisation en nombres premiers n’est pas un problème NP).
On ne peut ainsi pas se servir de nos raisonnements et algorithmes actuels, en bénéficiant juste de la puissance de calcul quantique.
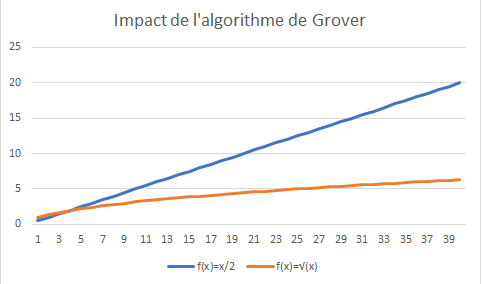
Il existe cependant une alternative : l’algorithme de Grover. Ce deuxième algorithme quantique le plus connu montre qu’avec un ordinateur quantique, la recherche de solution « au hasard », en testant si les solutions fonctionnent ou non, passe d’un nombre S/2 en moyenne à √(S), ce qui représente une belle diminution, même si cela reste insuffisant dans la pratique.
Ainsi, on ne sait pas si l’ordinateur quantique pourra nous aider à prouver que P=NP ou nous aider, si ce n’est pas le cas, à trouver des solutions aux problèmes NP dans un temps acceptable. Une chose est sûre cependant : c’est en exploitant la structure du problème que l’on pourra créer des algorithmes quantiques efficaces, nous permettant de bénéficier de la puissance de calcul de ces machines.
Pour conclure :
Les ordinateurs quantiques sont présents dans l’imaginaire collectif depuis un moment. Depuis beaucoup moins longtemps dans la réalité tant il est difficile d’en créer. En effet, les composants principaux, les qubits, ne sont pas si évidents à créer ainsi qu’à manipuler par la suite. De plus, le fonctionnement de ces machines suppose d’autres sortes d’algorithmes pour véritablement délivrer leur plein potentiel de calcul. Cela n’empêche pas de nombreuses sociétés comme Google, Microsoft, mais aussi des agences comme la NSA de continuer les recherches et de se rapprocher de la date de sortie d’un ordinateur fonctionnel. Ainsi, en mai 2017, IBM a présenté ses systèmes équipés de 16 et 17 qubits ! Un exploit quand on sait que les systèmes précédents n’en possédaient que 5…
Ainsi, bien qu’il ne faille pas s’attendre à pouvoir faire tourner The Elder Scrolls VI sur ces machines dans son salon, ces « calculateurs », plus qu’ « ordinateurs » quantiques, pourront bientôt nous aider dans nos recherches… A condition de savoir précisément quelle question poser (la réponse risquant sinon d’être systématiquement 42…).